Pourquoi et comment faire écrire les élèves ?

 Plan :

1. Pourquoi faire écrire les élèves ?

2. Place et rôle de l’écrit dans nos problèmes de recherche

3. Fonctions des écrits dans nos scénarii

4 Exemples d’exploitation d’écrits

5. Bibliographie

 

1. Pourquoi faire écrire les élèves ?

Inciter les élèves à écrire en mathématiques dans le cadre de la résolution de problèmes ou d’exercices, en dehors de la réponse finale, et de quelques bribes de brouillon, n’est en général pas dans les habitudes des professeurs. Et écrire en mathématiques en dehors de cela n’est pas non plus un geste naturel et facile pour les élèves. Pourtant des écrits intermédiaires ou complémentaires provoqués peuvent se révéler utiles pour leur permettre de chercher et de développer des solutions, puis de les rédiger et de les « digérer ». Ils permettent également de favoriser l’acquisition des savoirs visés à l’occasion de la résolution de ces problèmes et, bénéfice important, de développer les capacités d’expression et de communication.
Les écrits complémentaires sont non seulement utiles mais d’abord nécessaires car la rédaction des élèves ne nous permet pas toujours de comprendre les raisonnements sous-jacents.
Par exemple, en réponse à la recherche du signe de 𝑓(𝑥), on rencontre souvent des écrits de ce type sans autre forme d’explication :

Quel est le cheminement qui a amené l’élève à produire ce tableau ?Au fait que 𝑓(−7) ou la limite en −7 de 𝑓(𝑥) est effectivement négative ? ou au fait qu’il a vu −4 et du coup en a déduit que 𝑓(𝑥) est de signe négatif sans avoir vérifié la valeur de 𝑓(−7) ou la limite en -7 ? ou à la confusion entre signe et variation : 𝑓 décroissante et donc 𝑓 (𝑥) négatif ? ou à une autre idée, pertinente ou pas ?

En l’occurrence, on pourrait demander à l’élève d’expliquer comment il en est arrivé à ce tableau. On aurait alors une chance d’avoir davantage accès à ses représentations et lui-même aurait l’occasion de faire un retour réflexif sur ses connaissances, justes ou pas. De plus, une comparaison entre plusieurs explications produites par des élèves différents, permettrait à toute une classe d’entamer un débat qui rectifierait et développerait leurs connaissances. Exiger qu’une réponse ne se limite pas à des calculs ou à un tableau est primordial.
En fait, l’écrit est une composante essentielle de l’activité mathématique. Qu’enseigne-t-on ? Qu’apprend-on aux élèves ? Veut-on former des « automaths » comme le dit Stella Baruk (dans son livre « l’âge du capitaine ») ou veut-on former des citoyens qui raisonnent et savent argumenter au sens mathématique ? L’écrit permet, par exemple, de dépasser le simple traitement algorithmique des calculs et de redonner du sens aux concepts en jeu. Comme l’écrit le philosophe du 17ème siècle, Hobbes, « les symboles sont pauvre mesquinerie, même en tant que nécessaire échafaudage de démonstration. Les symboles, même s’ils raccourcissent l’écriture, ne font pas comprendre plus vite que si c’était écrit en mots… Car il y a un double travail de l’esprit, l’un de réduire les symboles en mots qui sont eux-mêmes symboles, l’autre d’atteindre aux idées dont elles sont le signe. »
Une page remplie de calculs n’est pas suffisamment révélatrice des compétences, des connaissances et savoir-faire acquis par l’élève et ne permet pas une évaluation correcte de ceux-ci.
Par exemple, l’élève qui résout une équation comme suit :

La technique semble maîtrisée mais qu’a-t-il retenu de cette résolution d’équation ? Quel sens donne-t-il à la dernière ligne ? Que signifie ce 𝑆 ? L’ensemble des solutions de l’équation ? La réponse à la question ? A-t-il compris que 0 et 3/7 sont les seuls nombres pour lesquels la première égalité est vraie ?
Comme le dit M.J. Perrin (Questions didactiques soulevées à partir de l’enseignement des mathématiques dans les classes faibles », p5 à 119, RDM, 1993) nous sommes convaincus que l’écrit a un rôle dans les processus d’apprentissage. N. Balacheff précisait (dans le bulletin A.P.M. 342 page 94, 1984) qu’il permet de réorganiser les connaissances acquises, d’étayer les apprentissages et de prendre de la distance par rapport aux tâches mathématiques immédiates.

2. Place et rôle de l’écrit dans nos problèmes de recherche

L’écrit et ses différentes modalités de production tiennent donc une place importante dans la conception de nos séances de résolution de problèmes de recherche, ainsi d’ailleurs que les articulations entre les phases d’écriture et les phases orales. Voici la structure générale de nos scénarii :

1.  Phase d’appropriation individuelle avec trace écrite
2.  Recherche individuelle avec possibilité d’échanges entre élèves, ou recherche en groupes avec production individuelle d’écrits
3. Comparaison et analyse des écrits judicieusement choisis de certains élèves
4. Poursuite de la recherche ou reprise des écrits pour les améliorer, soit du point de vue de la forme soit du point de vue du fond, suite à l’analyse de la phase 3

La phase 1 de courte durée (10 minutes environ), a pour but l’appropriation de l’énoncé du problème. Pour cela le contenu de la trace écrite attendue est laissé à l’initiative des élèves : cette trace peut être constituée, selon le cas, d’un schéma annoté, de quelques formules écrites, de questions par rapport aux parties non comprises de l’énoncé. Cet écrit doit permettre à l’élève de réfléchir de façon autonome pour comprendre le problème, voire d’envisager déjà sa résolution, et à l’enseignant de s’assurer de cette compréhension et de revenir si nécessaire sur l’énoncé du problème.
La production écrite individuelle attendue à la phase 2 relève de l’écrit de recherche 1 (Chevalier A ,1989 et Sauter M,1998). Il est demandé aux élèves de formuler leurs démarches, les idées qu’ils ont eues, explorées, pourquoi ils les ont abandonnées, etc…L’élaboration individuelle de cet écrit n’exclut pas la possibilité d’échanges entre élèves du même groupe, ni de moments d’échanges collectifs gérés par le professeur. Cette phase de travail oblige les élèves à prendre conscience de leur démarche, leur permet d’enrichir, de modifier, de développer leur raisonnement. Pour le professeur, c’est l’occasion de prendre connaissance des démarches des élèves et d’y réagir pour les accompagner mais non les diriger. A l’issue de cette phase, certains des écrits individuels seront sélectionnés par le professeur et serviront de base pour la phase 3.
Le professeur veillera à choisir des copies comportant à la fois des points à améliorer et des points positifs, soit du point de vue mathématique soit du point de vue rédactionnel. Lors du premier problème de recherche, il est nécessaire d’expliquer aux élèves que les écrits sont choisis parce qu’ils sont représentatifs d’un certain type de production et ont un intérêt pour la classe et non pour valoriser ou stigmatiser un élève en particulier.
Dans la phase 3, on montrera aux élèves cette sélection d’écrits anonymés. Cela leur permettra de remarquer ce qui manque à certains écrits pour qu’ils soient compréhensibles mais surtout de dégager avec eux les points essentiels : explication de chaque piste (ou fausse piste), bilan de la recherche, illustration éventuelle de la démarche par des schémas, suite du travail si le temps imparti était plus long. On veillera à ce que chaque élève ait une trace écrite de cet échange.
Dans la phase 4, selon l’état d’avancement de leur recherche à ce moment-là on pourra demander aux élèves soit de reprendre leur écrit en tenant compte du bilan et de prolonger leur recherche soit de rédiger la résolution complète du problème. Le but de cette phase est que chaque élève aboutisse à une rédaction améliorée de sa solution. L’idéal serait d’examiner et de comparer certaines de ces nouvelles rédactions parce que chacune présente encore des lacunes mais aussi des apports essentiels pour la rédaction finale de la solution (Adjiage R ; Rauscher JC, 2013, p23).
En général, les élèves ne connaissent pas tous cet écrit et il nécessite donc une initiation spécifique lors du premier problème de recherche fait dans l’année. Signalons d’ailleurs que ce type d’écrit est attendu au baccalauréat lors de questions dites « ouvertes » où il est précisé que « toute trace de recherche même incomplète sera prise en compte ». Depuis la session de juin 2015, on peut rencontrer une partie d’un problème qui ne sera plus guidée. Un écrit de recherche sera attendu afin de comprendre la démarche effectuée par l’élève.

3. Fonctions des écrits dans nos scénarii 

Au-delà de la description des scénarii que nous venons de faire, nous voudrions revenir plus précisément sur les fonctions principales des écrits qui jalonnent le travail des élèves dans la marche qui les mène vers la résolution de problèmes de recherche.
La fonction qui apparaît d’emblée la plus évidente est la fonction heuristique. Les écrits de recherche permettent de partager avec les autres élèves les idées de résolution et d’en générer d’autres. Ils permettent au professeur de connaître et d’accompagner ce développement heuristique.
Ces écrits permettent aussi au professeur de repérer les connaissances des élèves. L’analyse des écrits choisis et classés judicieusement permettra de faire prendre conscience aux élèves de l’intérêt de l’utilisation de certains outils déjà connus pour éventuellement les mener jusqu’à la nécessité de savoirs ou savoir-faire nouveaux. En particulier on veillera à classer les écrits en allant de la méthode la plus intuitive à la méthode la plus experte.

Enfin, c’est aussi la fonction de traitement que permet l’écrit dans sa matérialité qui est utilisée. Si les deux fonctions précédemment signalées se centrent en premier lieu sur les idées véhiculées par les écrits (idées de résolution, savoirs en jeu etc..), nous tablons ici sur « les possibilités cognitives spécifiques d’organisation et de contrôle qu’offre la représentation visuelle [car écrite] du discours » (Duval R. 2000). Nous entrons alors dans « la pratique écrite de l’écrit », cette pratique s’opposant à la « pratique orale de l’écrit », qui sert principalement à fixer ce qui a été dit ou à transcrire ce qu’on pense spontanément, sans recul. Les élèves sont pour cela invités à examiner la forme de leurs écrits pour en repérer les lacunes, les incohérences et les remanier. Raymond Duval et Marie-Agnès Egret (1989) ont développé cette approche dans le domaine de l’apprentissage de la preuve formelle en géométrie à l’aide de la représentation des démonstrations par des réseaux. On verra comment l’attention portée à la structure de leurs écrits permet aux élèves d’avancer dans leur compréhension et dans l’acquisition de nouvelles connaissances.

4 Exemples d’exploitation d’écrits

                    4.1 pour mettre en évidence la fonction heuristique de ces écrits

Voici venu le moment de montrer sur un exemple précis, le problème du Bonhomme, comment en nous appuyant sur leurs écrits, nous avons fait progresser les élèves dans la résolution d’un problème et à travers cette résolution dans le développement de leurs connaissances en mathématiques.
Le bonhomme
Niveau : 2nde (mais peut être donné dès la 3ème)
Enoncé :

Objectif : représenter une quantité exprimée en fonction d’une autre quantité à l’aide d’une courbe, ou déterminer le minimum d’une quantité ou d’une fonction, ou comprendre ce que signifie qu’une quantité varie en fonction d’une autre quantité

Prérequis : aire d’un disque, aire d’un carré

Notions abordées et travaillées dans le problème : variable, tableau de valeurs, courbe,
expression algébrique, minimum, variation

Un exemple d’exploitation des écrits des élèves lors de la résolution de ce problème (phase 3):
Une première sélection d’écrits a été projetée pour permettre aux élèves de les analyser et de les comparer. Il leur est alors apparu que les tableaux étaient une façon commode d’organiser leurs investigations. Nous allons voir maintenant comment sur une deuxième sélection d’écrits les remarques positives comme négatives des élèves permettent à ceux-ci de progresser vers les objectifs visés.
Ecrit 1

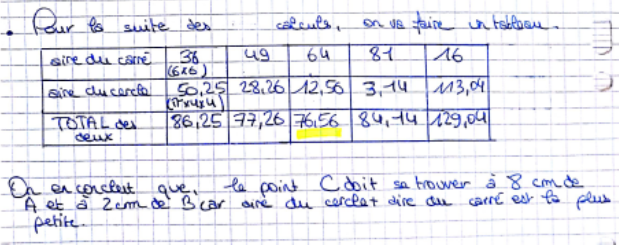
Remarques formulées par les élèves :
 le fait que le point C se trouve à 8 cm du point A n’apparaît pas dans le tableau
 le tableau donne l’aire totale de la figure (ce qui n’est pas le cas dans tous les écrits, parfois
seules les aires du carré et du cercle étaient notées dans le tableau.
 les valeurs des aires sont incorrectes, ils ont confondu rayon et diamètre.

Ecrit 2

Remarques formulées par les élèves :
 ce tableau donne l’aire totale de la figure et la longueur AC ce qui permet de relier la
position de C à l’aire totale
 la conclusion de ce groupe ne donne pas la position du point

L’objectif visé par la critique des deux écrits précédents est de faire prendre conscience aux élèves que regrouper les valeurs calculées dans un tableau demande une réflexion quant aux quantités qui sont à présenter dans un tel tableau : repérer la quantité étudiée (ici l’aire) et de quelle quantité (ici la longueur du côté [AC] du carré) dépend la première.Lors de l’analyse des écrits suivants 3 et 4  l’objectif est que, via les critiques, les élèves repèrent de nouvelles idées ou démarches.

Ecrit 3

Par rapport à certains écrits dans lesquels les deux aires étaient calculées séparément puis ajoutées, apparaît ici le regroupement dans une seule égalité des deux aires

Ecrit 4

Dans cet écrit c’est le fait que les deux aires de la tête et du corps s’expriment toutes les deux en fonction d’une même variable (diamètre du cercle) qui sera mis en avant.

De plus dans l’écrit 4, le tableau met en relation l’aire totale en fonction du diamètre du cercle, la variable choisie (côté du carré pour les écrits précédents et diamètre du cercle pour celui-ci) n’est donc plus la même mais l’aire minimale est identique à celle trouvée dans les autres écrits.

Les remarques formulées sur ces écrits par les élèves et le débat qui a suivi ont permis de dégager  plusieurs démarches:

• une démarche (A) (écrit 1) où plusieurs aires sont calculées et présentées de façon organisée dans un tableau (aire du carré, aire du disque, total des deux) mais où n’apparait pas la dépendance de l’aire totale par rapport à une des longueurs.

• une démarche (B) (écrit 2) où apparaît la dépendance de l’aire totale par rapport à une des longueurs (rayon ou diamètre du cercle, longueur du côté du carré) mais toujours dans le registre des tableaux

• une démarche (C) (écrit 3,4) où est introduite et utilisée une seule variable  pour décrire la dépendance de l’aire totale en fonction de cette variable et dans laquelle en regroupant les deux idées mises en avant on obtient une expression de l’aire en fonction d’une seule variable. La dépendance est alors exprimée dans le registre algébrique.

 

Nous voyons que ces comparaisons permettent aux élèves de s’approprier la façon de construire un tableau de valeurs ainsi que la notion de variable, et de comprendre ce que signifie qu’une quantité varie en fonction d’une autre.

Nous n’avons donné ici qu’un exemple d’exploitation possible des productions écrites des élèves lors de la résolution du problème du Bonhomme. Pour une présentation plus complète, nous renvoyons le lecteur au document d’expérimentation « Le Bonhomme ».

4.2 pour décrire la fonction de traitement des écrits

Voici un exemple sur le problème du « Triangle » où un écrit a été repris pour permettre aux élèves de dépasser une « pratique orale de l’écrit » pour entrer dans « une pratique écrite de l’écrit ». La pratique orale de l’écrit consiste à produire un premier jet de ce que l’on veut dire, premier jet qui laisse sous-entendu certains éléments du raisonnement et ne fait pas ou peu apparaître les articulations logiques entre les éléments. Ce premier jet par son incomplétude ne permet en général pas d’apprécier la validité du raisonnement de l’élève.  Il s’agit alors de donner aux élèves l’occasion de retravailler ce premier jet pour le réorganiser, le compléter, non pas seulement pour obtenir « un écrit plus satisfaisant », mais surtout pour leur donner la chance de s’approprier pleinement un raisonnement complet.

Niveau : 2nde ^nde

Enoncé : OAB est un triangle rectangle  en O où OA mesure 2 cm et OB 16 cm.

M un point de [OA], N un point de [OB] tel que BN est égal à 7 fois  OM.

Où placer exactement le point M sur [OA] pour que l’aire du triangle OMN soit maximale?

 Objectif : démontrer qu’une expression du second degré admet un extremum

Ci-contre l’écrit produit

par un groupe à la fin de

la première séance :

La valeur exacte du maximum n’a pas été déterminée mais comme il s’agissait d’introduire cette notion par ce problème, ce n’était pas un attendu de la première séance.

Le raisonnement développé par ces élèves semble correct, l’expression de l’aire du triangle et la démarche pour obtenir une valeur approchée de l’aire maximum sont justes. Malgré cela ce genre d’écrit ne peut être considéré comme un écrit final et il est donc nécessaire de le retravailler.

Voici une manière de le reprendre, elle prend appui sur la pratique (décrite dans le paragraphe 3 -Fonctions des écrits dans nos scénarii- et décrivant la fonction de traitement des écrits) que R. Duval et M.A.Egret utilisaient pour améliorer la forme des écrits lors de démonstration en géométrie.

Les élèves critiquent  par écrit et individuellement la production de ce groupe qui leur a été distribuée, puis un débat a lieu sur ce qui est correct et ce qui est à améliorer.

A partir de ces critiques, on entoure dans cet écrit les hypothèses dans une couleur (ci-dessous en vert), les conclusions dans une autre (ci-dessous en bleu) et les propriétés dans une troisième (ci-dessous en rouge). Lorsque cela est suffisamment clair dans l’écrit initial, on ajoute des flèches reliant les différentes informations. Le réseau ainsi obtenu est celui représentant le texte initial du groupe. Les couleurs permettent de visualiser le changement de statut des différentes propositions.

L’absence de flèche  partant ou arrivant à une information ou le fait que la conclusion n’est reliée à aucune hypothèse  nous permet d’affirmer que nous ne pouvons valider un tel réseau. Sous forme de débat avec les élèves, ils essaient  donc de trouver ce qu’il faut ajouter et comment relier toutes les informations écrites. Le début de ce travail est fait avec les élèves puis ils le poursuivent individuellement. On le finalise au tableau ensemble.

Voici le réseau finalisé de la partie d’un écrit menant à l’expression de l’aire du triangle OMN.

Le travail présenté est un travail préparatoire à la forme de l’expression écrite, mais en travaillant sur la structure du raisonnement, on produit en fait également un travail sur le fond. Il permet à certains élèves qui n’arrivent pas encore à produire un raisonnement rédigé de mieux comprendre les différentes étapes de ce raisonnement.

Après cette analyse on demande aux élèves de rédiger le raisonnement.

Voici un exemple de texte produit par un élève à la suite de ce travail :

Ce texte traduit bien le réseau que nous avions produit ensemble. Par rapport au premier texte où il manquait de nombreuses explications, dans celui-ci les explications  pourraient être considérées  comme trop fournies. Mais il s’agit là d’une phase essentielle où l’on voit bien que l’élève est en train de s’approprier vraiment un raisonnement complet. Ecrire un texte comportant les explications nécessaires et suffisantes n’est pas simple pour un élève. Par la suite il pourra apprécier lui-même  comment cette rédaction peut s’alléger.

5. Bibliographie

ADJIAGE R., RAUSCHER JC. (2013), Résolution d’un problème de modélisation et pratique écrite de l’écrit, dans Recherches en didactiques des mathématiques, volume 33/1, La pensée sauvage –éditions, p9 à 39
BUTLEN D., PEZARD M. (2003) Etapes intermédiaires dans le processus de conceptualisation en mathématiques. Recherche en Didactique des Mathématiques 23(1) 41–78.
CHEVALIER A. (1989) “Narration de recherche” en classe de quatrième : influence sur les stratégies et la motivation des élèves in Actes de la 41ème rencontre CIAEM.
CHEVALIER A. (1993) Un nouveau type d’exercices scolaire. Petit x 33 71–79.
DUVAL R., EGRET M.A. (1989) Comment une classe de quatrième a pris conscience de ce qu’est une démarche de démonstration. Annales de Didactique et de Sciences Cognitives de l’IREM de Strasbourg 2 41–64
RAUSCHER JC. (2006) L’écriture réflexive au centre de l’activité mathématique dans la résolution de problèmes de proportions. Annales de Didactique et de Sciences Cognitives de l’IREM de Strasbourg 11 75–102.
RAUSCHER JC. (2006) Écrire en mathématique pour situer et négocier les écarts. Un outil d’évaluation partagé. In Hélot et al. (Eds.) Écarts de langue, écarts de culture (pp.87–102). Frankfurt am Main : Peter Lang.
SAUTER M. (janvier 1998), Narration de recherche, une nouvelle pratique pédagogique dans Repères n° 30, Topique éditions, p. 9 à 21
VYGOTSKI L. (1934) Pensée et langage. Rééd. 2002. Paris : La Dispute.